
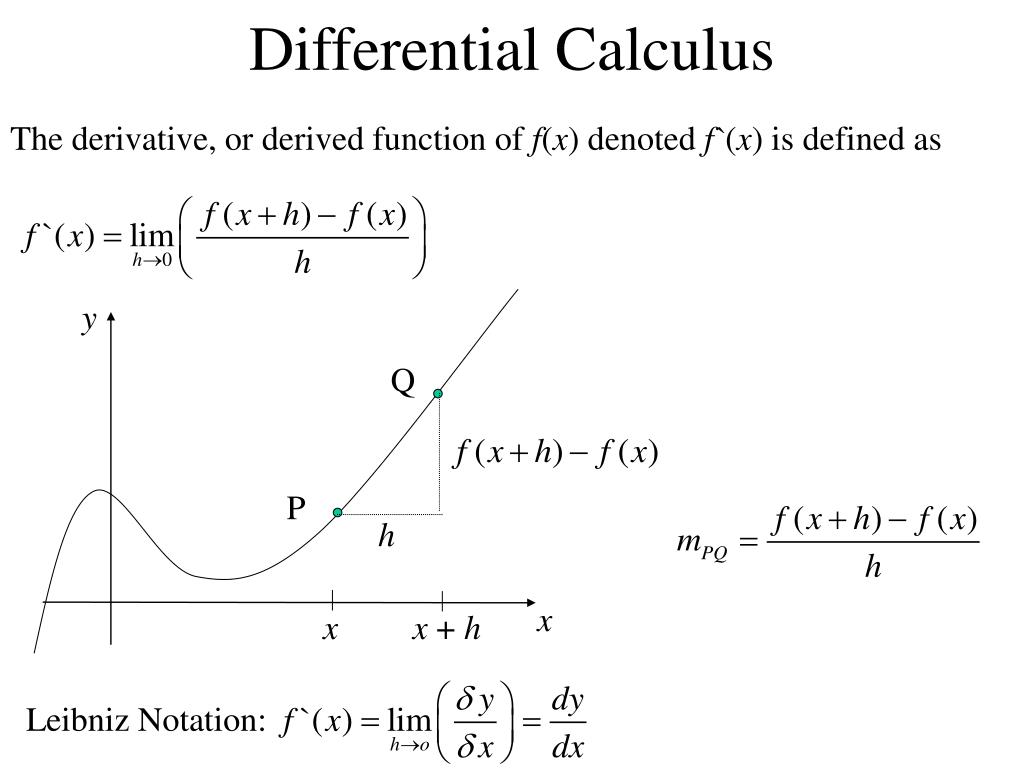
The slope(m) of the tangent to a curve of a function y = f(x) at a point \((x_1, y_1)\) is obtained by taking the derivative of the function (m = f'(x) ).īy finding the slope of the tangent line to the curve and using the equation \(m = (y - y_1)/(x - x_1) \), we can find the equation of the tangent line to the curve. A tangent is a line to a curve that will only touch the curve at a single point and its slope is equal to the derivative of the curve at that point. If we have a curve of a function and we want to find the equation of the tangent to a curve at a given point, then by using the derivative, we can find the slope and equation of the tangent line. The equation of tangent and normal line to a curve of a function can be calculated by using the derivatives. Hence by using derivatives, we can find the linear approximation of function to get the value near to the function. This value is very close to the actual value of √(9.1) Putting a = 9 in L(x) = f(a) + f'(a)(x−a), we get, We will find the value of √9 and using linear approximation, we will find the value of √9.1. Here we have the function: f(x) = y = √x. Let us understand this with an example, we can estimate the value of √9.1 using the linear approximation. The tangent will be a very good approximation to the function's graph and will give the closest value of the function. The equation of the function of the tangent is The linear approximation method was given by Newton and he suggested finding the value of the function at the given point and then finding the equation of the tangent line to find the approximately close value to the function. Hence the derivative gives the instantaneous rate of change of a function within the given limits and can be used to find the estimated change in the function f(x) for the small change in the other variable(x).ĭerivative of a function can be used to find the linear approximation of a function at a given value. This means, if we want to find the small change in a function, we just have to find the derivative of the function at the given point, and using the given equation we can calculate the change. Now, for a very small value of h, we can write
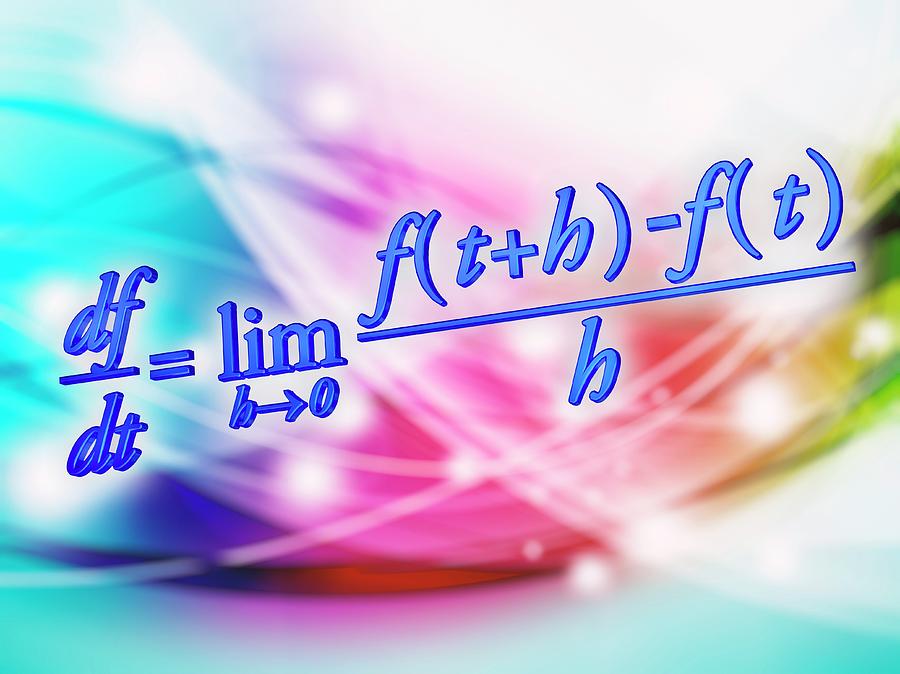
Which is also the instantaneous rate of change of the function f(x) at a. Now using the definition of derivative, we can write

Assume we have a function y = f(x), which is defined in the interval, then the average rate of change in the function in the given interval is By using the application of derivatives we can find the approximate change in one quantity with respect to the change in the other quantity. Derivative for Rate of Change of a Quantityĭerivatives are used to find the rate of changes of a quantity with respect to the other quantity.


 0 kommentar(er)
0 kommentar(er)
